Visibility Library

VisLib is a new, efficient C++ software library for solving visibility problems in the plane and in 1.5-dimensional terrains. VisLib contains a few highly complex algorithms, completely reimplemented and dispensing entirely with the use of inefficient and inaccurate trigonometric functions. Instead, it works with the orientation of points, derived from the cross product of vectors. Currently, only real coordinates of the double data type are used. An extension to rational coordinates is possible. Most algorithms are capable of visualizing themselves, thereby facilitating the communication of their mode of operation and troubleshooting.

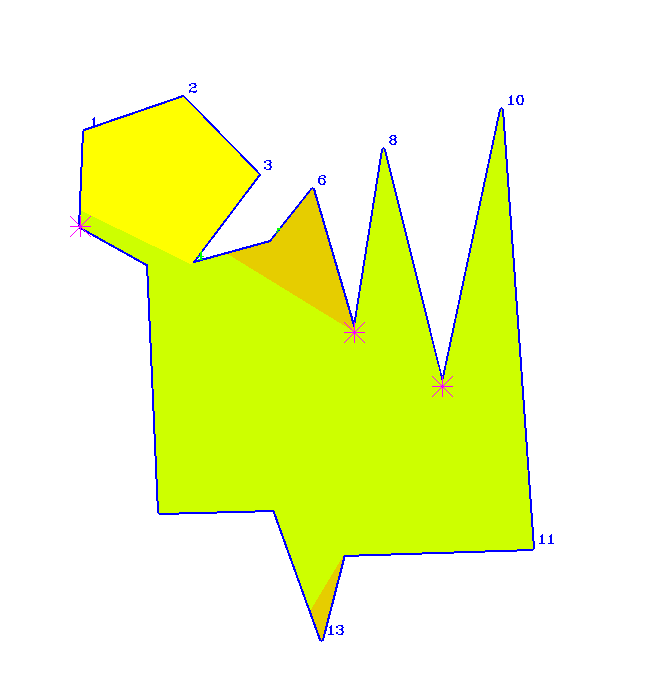
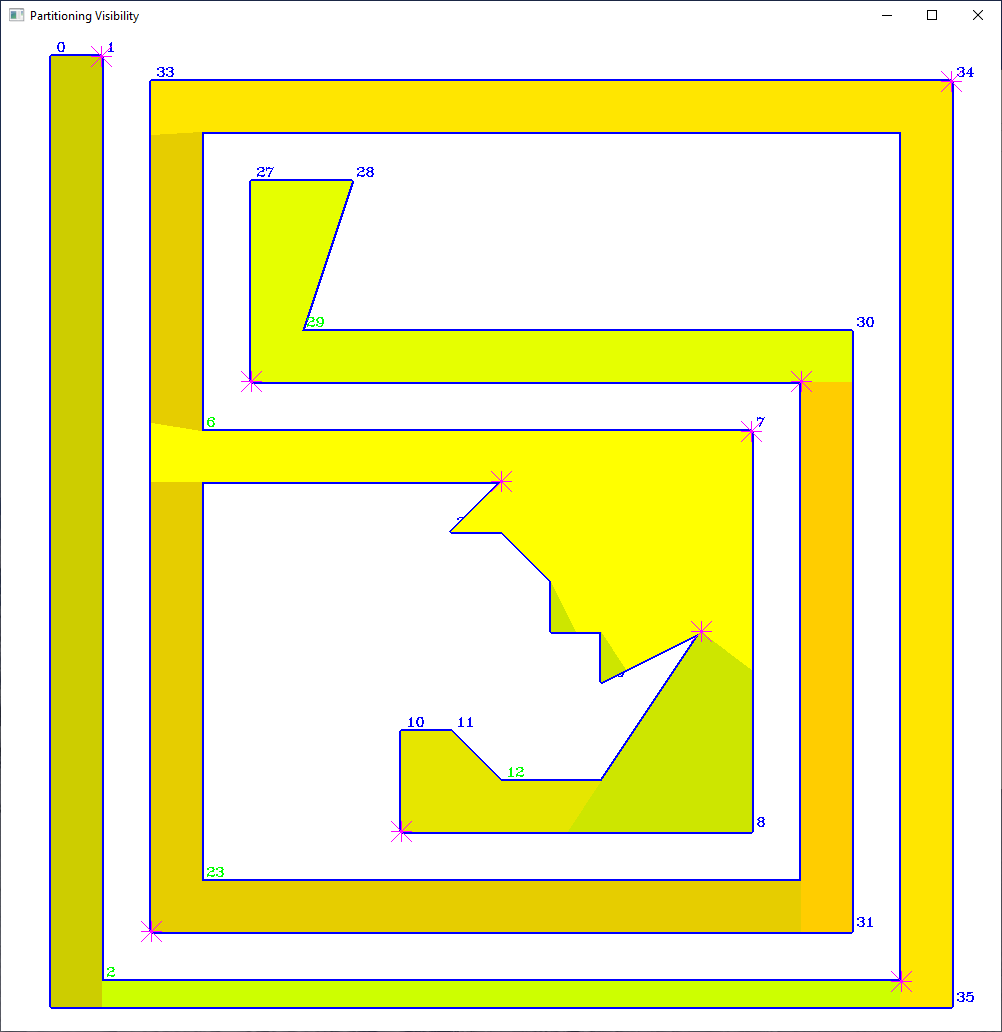
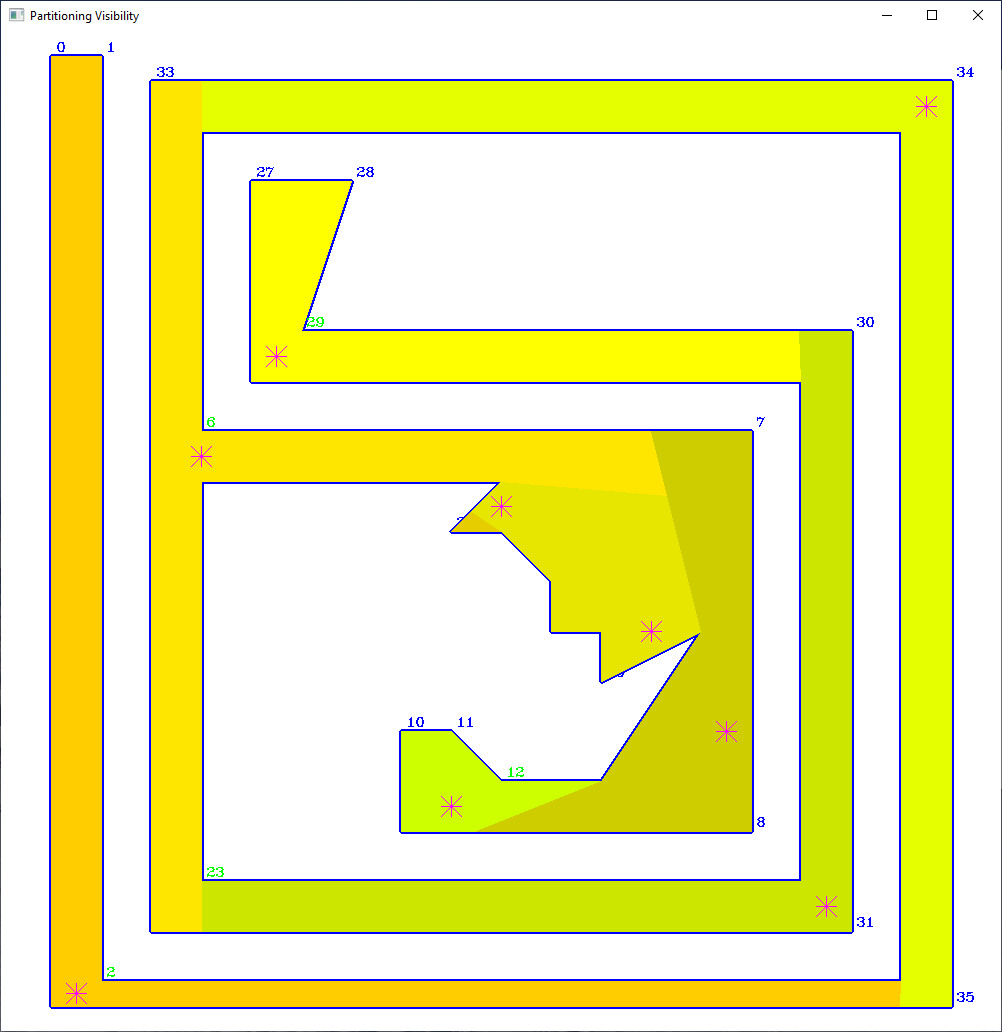
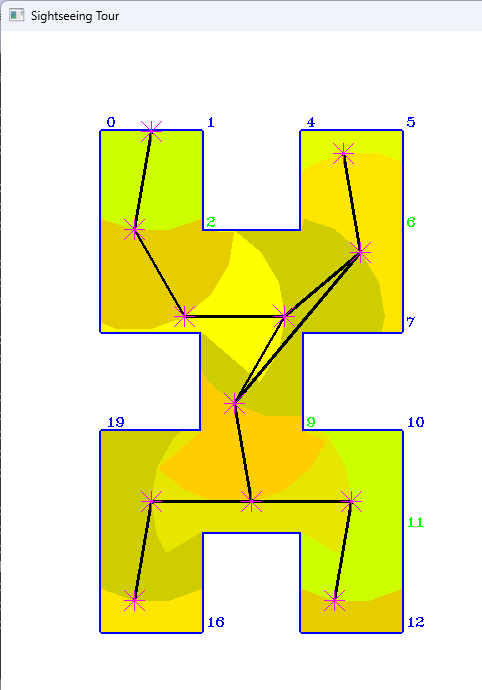
VisLib was developed in C++20 with the aim of making efficient visibility algorithms usable for pathfinding in robotics. With the existing visibility algorithms, it is possible to find short paths through polygonal spaces so that all vertices or edges of the polygon are seen.

Using Boolean operations on polygons, it is also possible to reduce the viewing distance to any desired distance, thereby solving practically relevant visibility problems.

HighGUI from OpenCV is used to visualize the algorithms and data. VisLib has no further dependencies.

Abstract Data Types

The following abstract data types are included in VisLib:

Point
Rectangle
Segment (line segment) with line segment intersections
SimplePolygon
Polygon (general polygon) with Boolean set-operations
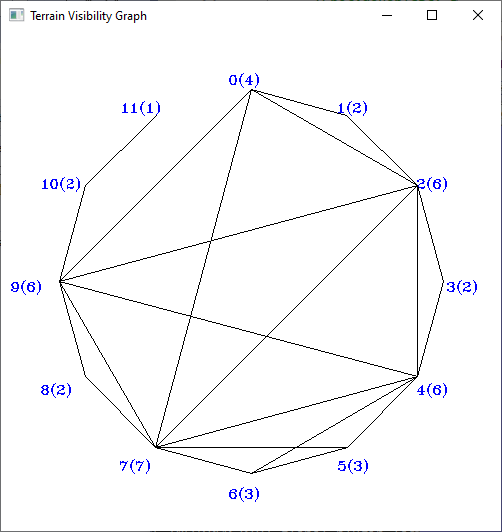
Terrain (1.5-D)
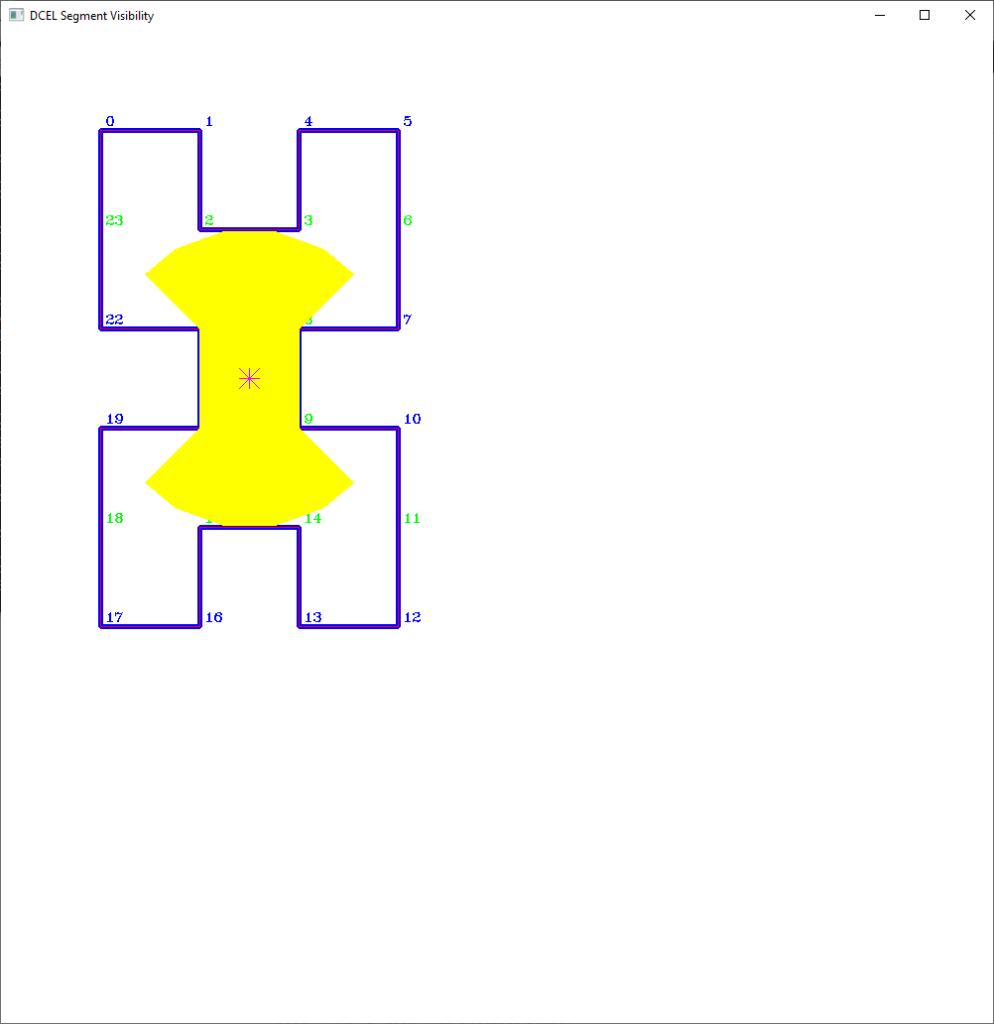
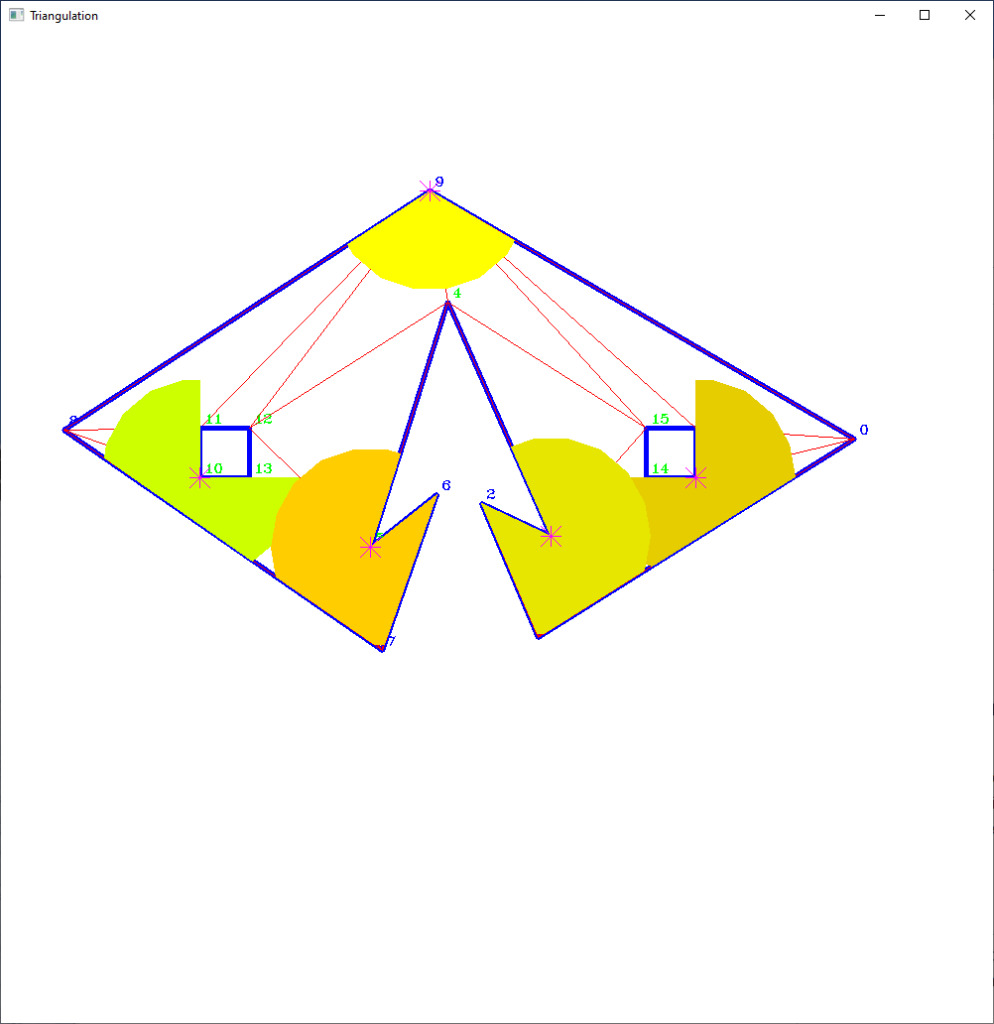
DCEL (doubly connected edge list) with (Delaunay) triangulation and dual-graph
Map (visibility map with shortest paths) based on DCEL
Overlay of two DCELs
IntervalTree
PriorityQueue with updatePriority
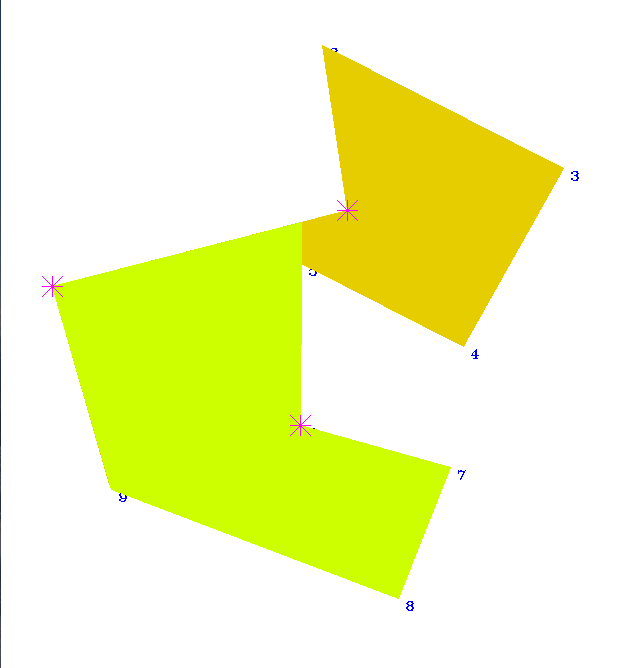
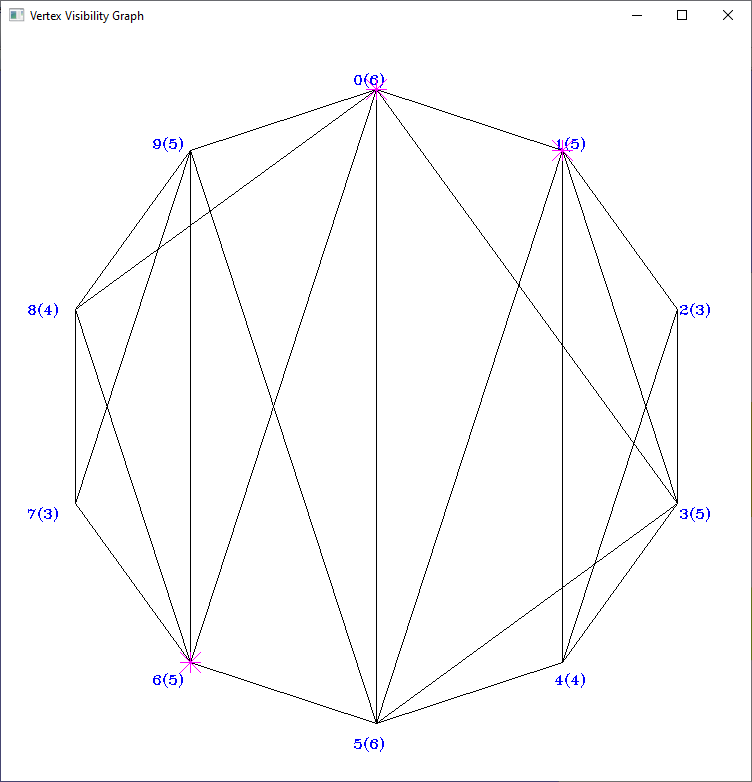
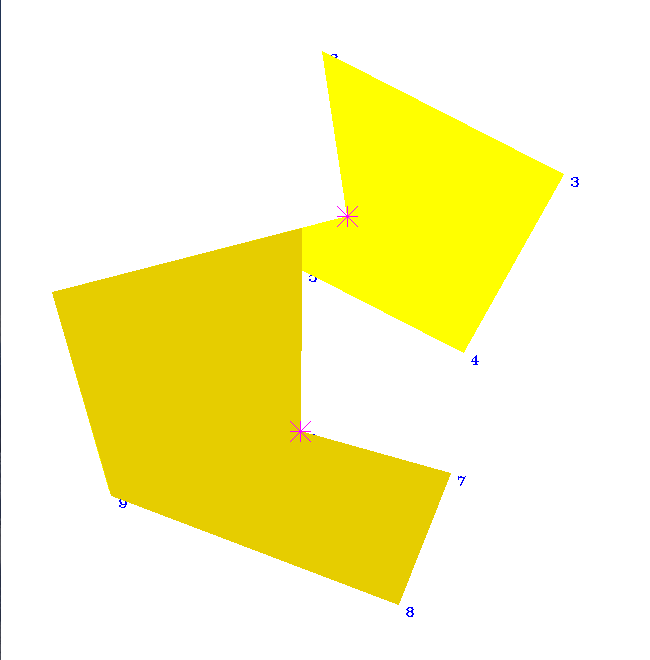
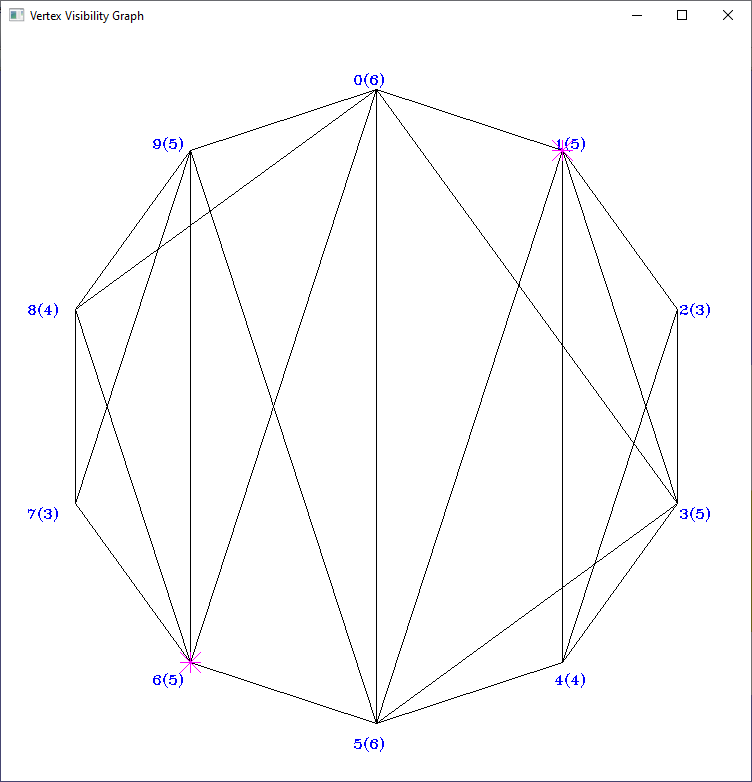
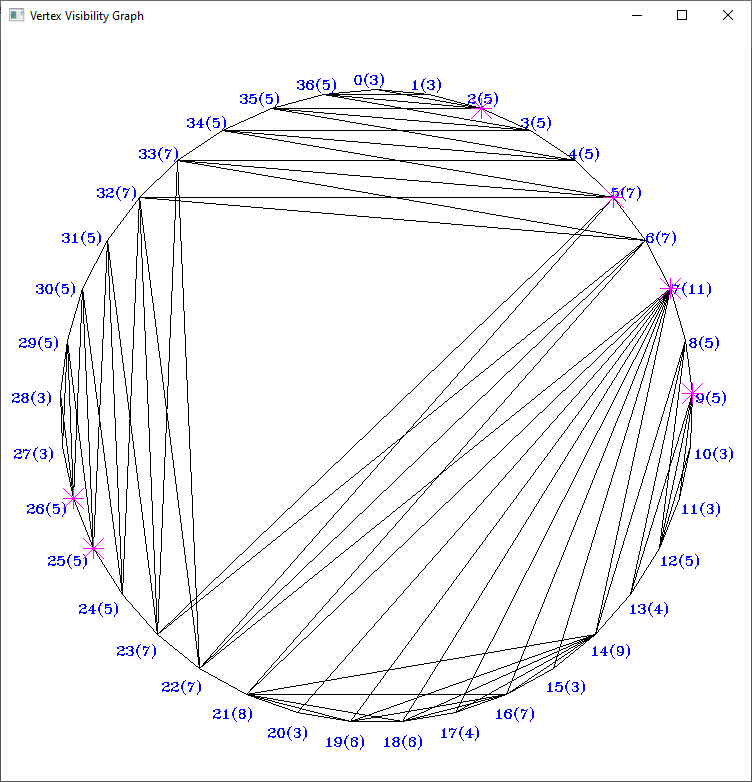
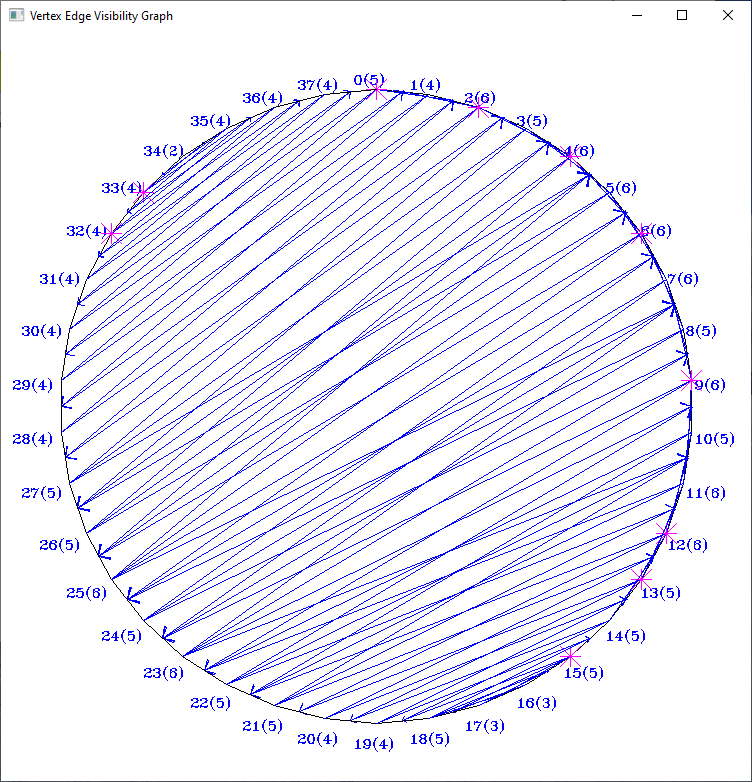
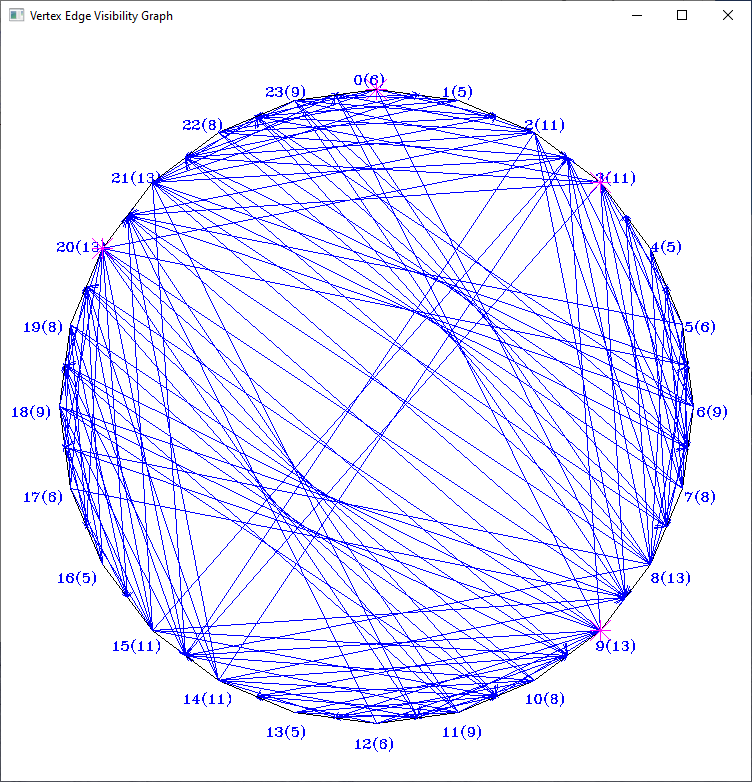
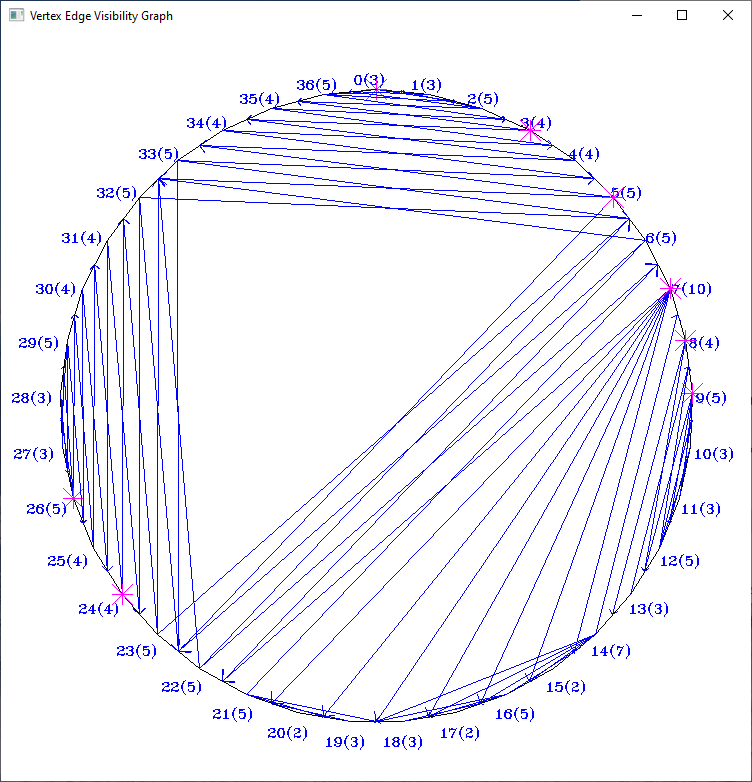
VisibilityGraph (vertex visibility graph): an edge of the graph expresses that one polygon vertex sees another polygon vertex in a simple polygon
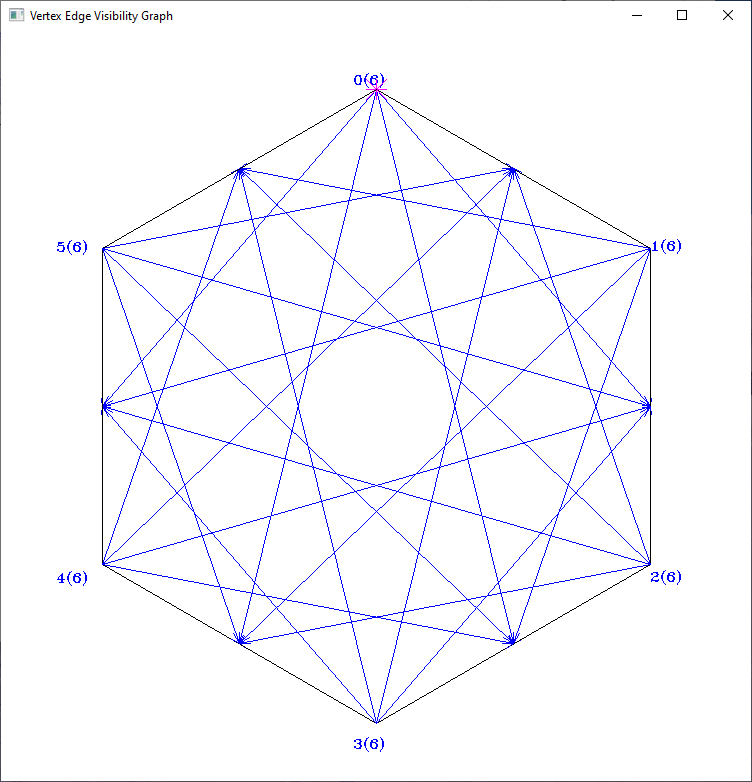
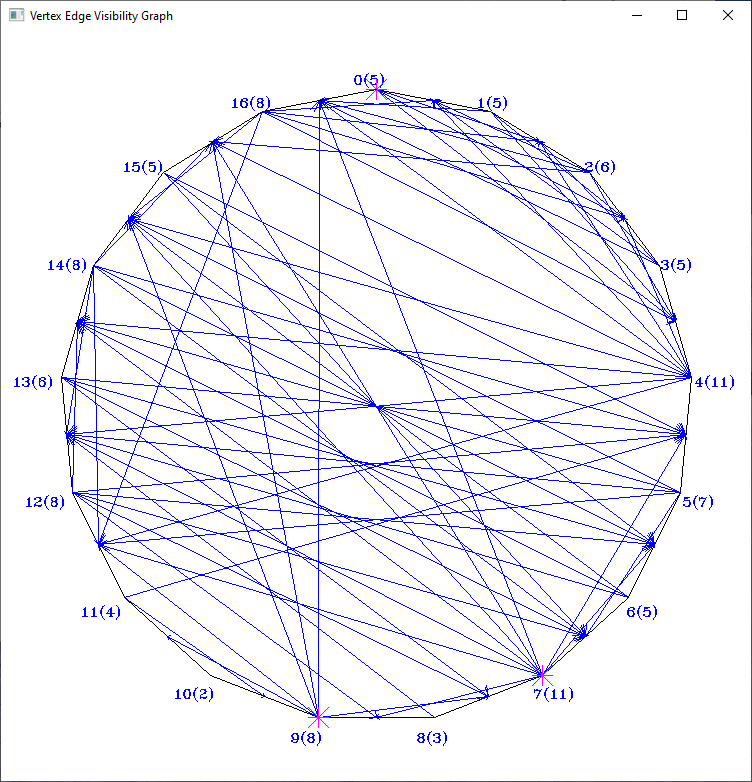
VertexEdgeVG (vertex-edge visibility graph): an edge of the graph expresses that a polygon vertex sees both endpoints of an edge (and thus the entire edge) in a simple polygon

Visibility Algorithms

The following visibility algorithms are included in VisLib:

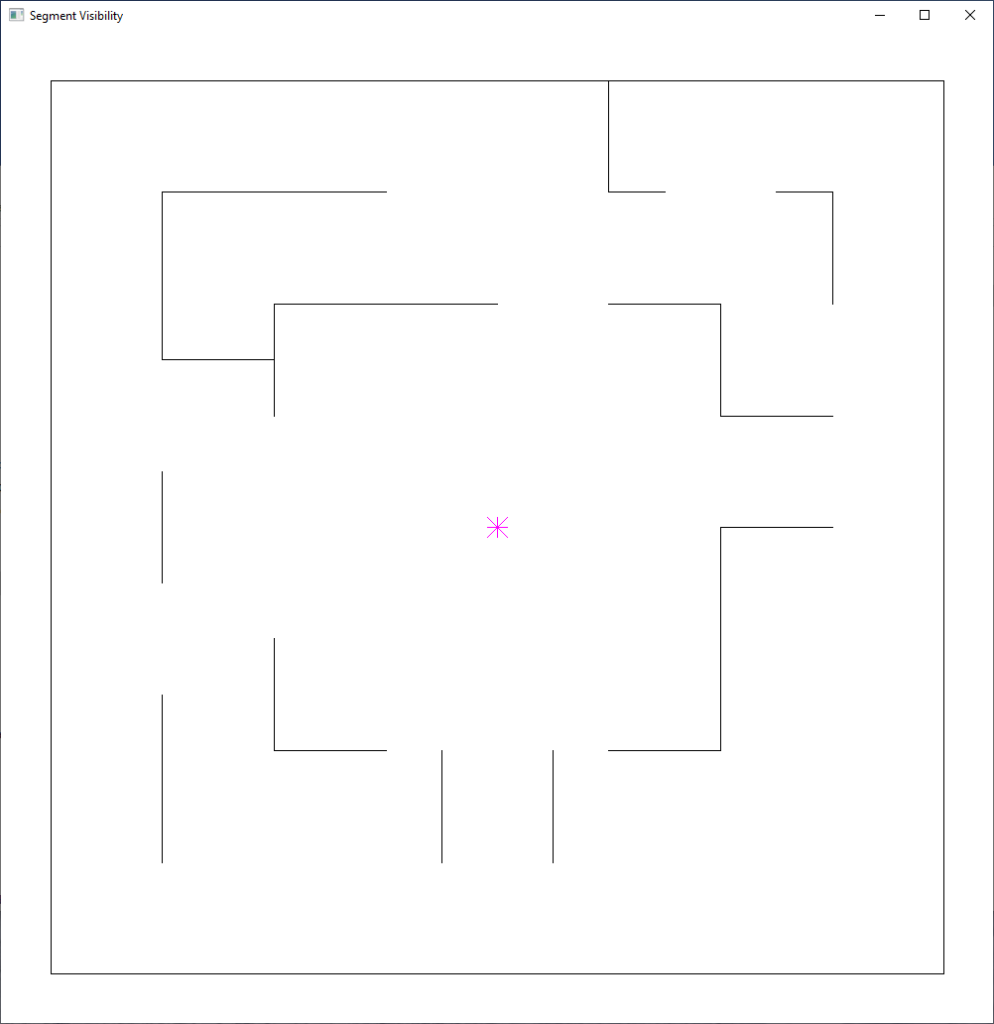
Segment Visibility: O(n log n), where n is the number of line segments
- T. Asano. An efficient algorithm for finding the visibility polygon for a polygonal region with holes. IEICE Transactions (1976-1990), (9):557–559, 1985.
- improvements:
  - using Cartesian coordinates instead of polar coordinates (no angle calculations are required)
  - no unnecessary line segment intersections are computed
  - angular sweep line range can be restricted (allows viewpoints directly on line segments)
Vertex Visibility in a triangulated simple polygon: O(n + m), where n is the number of polygon vertices and m is the number of edges in the vertex visibility graph
- Guibas, L., Hershberger, J., Leven, D. et al. Linear-time algorithms for visibility and shortest path problems inside triangulated simple polygons. Algorithmica 2, 209–233, 1987.
- Hershberger, J. An optimal visibility graph algorithm for triangulated simple polygons. Algorithmica 4, 141–155, 1989.
- improvements:
  - no angle calculations are required
  - regularized visibility for collinear points
  - abandoning finger search trees and replacing them with linked arrays, which enable exponential search without compromising runtime optimality
Simple Polygon Visibility: O(n), where n is the number of polygon vertices
- D. T. Lee. Visibility of a simple polygon. Computer Vision, Graphics, and Image Processing, 22:207–221, 1983.
- B. Joe and R.B. Simpson. Corrections to lee’s visibility polygon algorithm. BIT, 27:458–473, 1987.
- improvements:
  - no rotation of the coordinate system
  - no angle calculations are required for computing the angular displacements
1.5-D Terrain Visibility

Covering Algorithms

The following coverage algorithms are included in VisLib:

Minimum dominating set approximation (greedy) in a vertex-vertex visibility graph: O(n+ k*m), where n is the number of polygon vertices, k the number of selected vertices and m the number of graph edges
Minimum dominating set approximation (greedy) in a vertex-edge visibility graph: O(n+ k*m), where n is the number of polygon vertices, k the number of selected vertices and m the number of graph edges
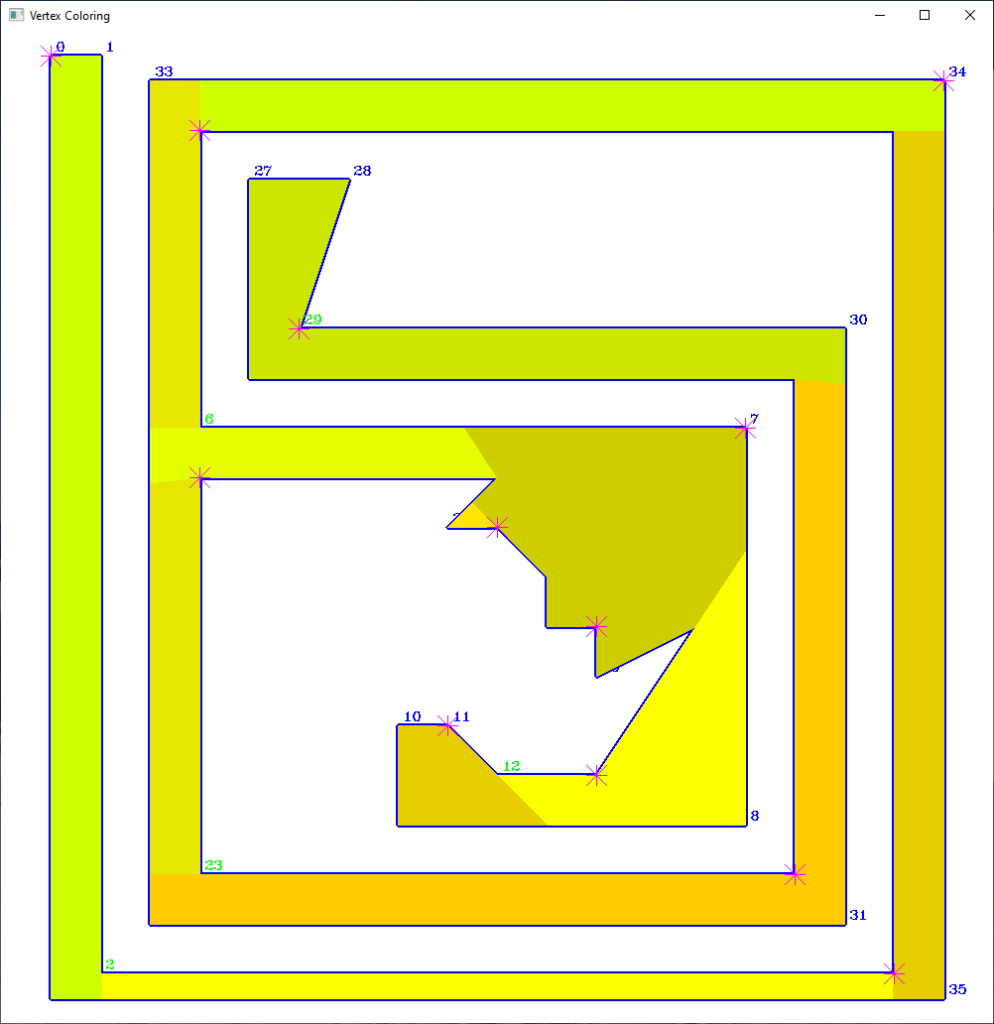
Vertex 3-Coloring in a triangulated simple polygon: O(n), where n is the number of polygon vertices
Non-optimal Convex Partitioning of a triangulated polygon with viewpoints on vertices or diagonals: O(n), where n is the number of polygon vertices