Aufteilen der Renderinggleichung
Gemäss Jim Kaija [11] kann eine physikalisch korrekte globale Beleuchtung mit einem rekursiven Integral beschrieben werden. Diese berühmte Gleichung wird Rendering Gleichung genannt und sieht wie folgt aus:
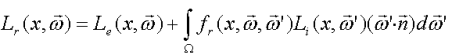
mit
- Lr(x,w) : Reflektierte Strahldichte zum Betrachter am Punkt x
- Le(x,w) : Selbstleuchtende Strahldichte zum Betrachter am Punkt x
- fr(x,w,w›) : Bidirktionale Reflexions Distributions Funktion am Punkt x
- Li(x,w›)(w•n) : Einfallende Strahldichte am Punkt x proportional zum Cosinus vom Winkel zw. n und w› (=w•n)
- n : Normale am Punkt x
- w : normalisierter Vektor vom Punkt x zum Betrachter
- w› : normalisierter Vektor vom Punkt x zum einfallenden Licht
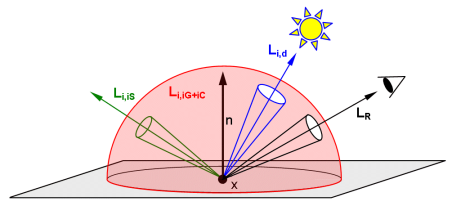
Dieses Integral lässt sich in verschiedene Teilintegrale unterteilen. Dies entspricht der Aufteilung des Problems in verschiedene Teilprobleme, die separat zu behandeln sind. Die Aufteilung des Domains, in diesem Fall die Hemisphäre in Subdomains ist eine Form des sogenannten Stratified Sampling. Das Aufteilen erfolgt gemäss den einfallenden Beleuchtungsbeiträgen Li, man betrachtet also, aus welchen Richtungen Beleuchtungsbeiträge zu erwarten sind. Wir unterscheiden zwischen direkter und indirekter Beleuchtung, die zusammen die volle globale Beleuchtung ergeben:
- Die direkte Beleuchtung Li,d betrifft die direkte Beleuchtung durch Lichtquellen.
- Die indirekte Beleuchtung Li,i*
andererseits betrifft alle Beleuchtungsbeiträge, die eben nicht direkt
von der Lichtquelle stammen. Diese können wiederum unterteilt werden in:
- Rekursive Anteile Li,iS durch Verfolgen der spekulären Richtung, resp. der transmittierten Richtung vom Auge aus. Dies ergibt die spekuläre Interaktion, wie wir sie vom Whitted Ray Tracer kennen.
- Indirekte Beleuchtung Li,iG und Li,iC durch Umgebungslicht, die wir anhand der Radiance Estimate mit der globalen und der Kaustik-Photonmap berechnen.

Die direkte Beleuchtung liefert den grössten Beitrag. Die Decke ist komplett schwarz, weil sie nicht direkt beleuchtet wird. Die beiden Kugeln liefern keinen direkten Beitrag, da sie 100% spiegelnd, resp. transparent sind.

Bei den Kugeln, werden die Strahlen rekursiv gespiegelt, resp. transmittiert. Treffen sie in der Folge auf eine diffuse Oberfläche, wird dort wiederum die gesamte globale Beleuchtung, d.h. die direkte, wie die indirekte Beleuchtung berechnet und zurückgeliefert.

Die indirekt diffuse Beleuchtung aus der globalen Photonmap. Wegem dem grossen Suchradius in der Photonmap ergibt sich ein weicher Verlauf.

Die indirekt diffuse Beleuchtung aus der Kaustik-Photonmap. Wegen dem kleinen Suchradius ergeben sich scharfe Kaustiken am Boden und an der rechten Wand. Durch die geringe Photonendichte an der Rückwand entstehen dort jedoch leichte Wolken.