Tech-Talk: Kalman Filter

Stellen Sie sich vor, Sie verfolgen eine Drohne durch dichten Nebel. Ihre Sensoren liefern verrauschte und gelegentlich irreführende Daten. Wie können Sie trotzdem zuverlässig bestimmen, wo sich die Drohne gerade befindet?

Die Antwort darauf liefert ein eleganter mathematischer Algorithmus: der Kalman-Filter, erstmals 1960 von Rudolf E. Kalman vorgestellt. Er dient dazu, den aktuellen Zustand eines dynamischen Systems – etwa Position, Geschwindigkeit oder Temperatur – aus ungenauen und verrauschten Messdaten möglichst genau abzuleiten. Heute ist der Kalman-Filter eine zentrale Methode der modernen Schätzungstheorie und wird in zahlreichen Anwendungsbereichen eingesetzt, unter anderem in der Navigation (z. B. GPS-Tracking), der Computer Vision, der Radar- und Zielverfolgung, der Wettervorhersage sowie in Robotik und Regelungstechnik.

Was macht der Kalman-Filter?

Im Kern löst der Kalman-Filter das Problem der Zustandsschätzung: Er bestimmt aus indirekten oder ungenauen Messungen den inneren Zustand eines Systems, beispielsweise die genaue Position eines Objekts trotz unsicherer GPS-Daten. Dabei arbeitet der Filter optimal, indem er die geschätzte Unsicherheit (Varianz) im Zeitverlauf minimiert. Voraussetzung ist, dass das zugrundeliegende System linear ist und das Messrauschen normalverteilt (gaussförmig) auftritt.

Vom Alpha-Beta-Filter zum Kalman-Filter: Ein einfacher Einstiegspunkt

Wie auch der Kalman-Filter kann der Alpha-Beta-Filter als einfacheres Verfahren zur Schätzung von Position und Geschwindigkeit eines Objekts anhand verrauschter Messdaten verwendet werden.

Er arbeitet in zwei Schritten:

1. Vorhersage der nächsten Position basierend auf der aktuellen Geschwindigkeit.
2. Aktualisierung von Position mit der neuen Messung.

Zwei Parameter steuern diesen Vorgang:

• Alpha (α): Wie stark man der Messung bezüglich der Position vertraut
• Beta (β): Wie flexibel man die Geschwindigkeit anpasst

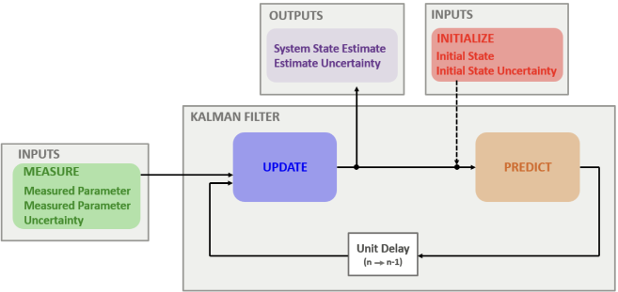
Obwohl dieser Algorithmus einfach und schnell ist, geht er von konstanter Geschwindigkeit aus und erfordert manuelle Anpassung der beiden Hyperparameter. Er modelliert Unsicherheit nicht explizit, bringt aber die zentrale Idee des Kalman-Filters ein: die Kombination von Vorhersage und Korrektur. Der Kalman-Filter erweitert diesen Ansatz, indem er die Gewichtung automatisch anhand der Unsicherheit anpasst, Beschleunigungen berücksichtigt und mit mehreren Variablen umgehen kann. Messwerte werden nun als normalverteilt um einen wahren Wert angenommen. Das vereinfacht die Mathematik und entspricht vielen Messquellen mit natürlichem Rauschen.

Feinabstimmung mit dem Kalman-Gain

Eine der intelligenten Eigenschaften des Filters ist der Kalman-Gain, ein Faktor, der bestimmt, wie stark die neue Messung im Vergleich zur Vorhersage gewichtet wird.

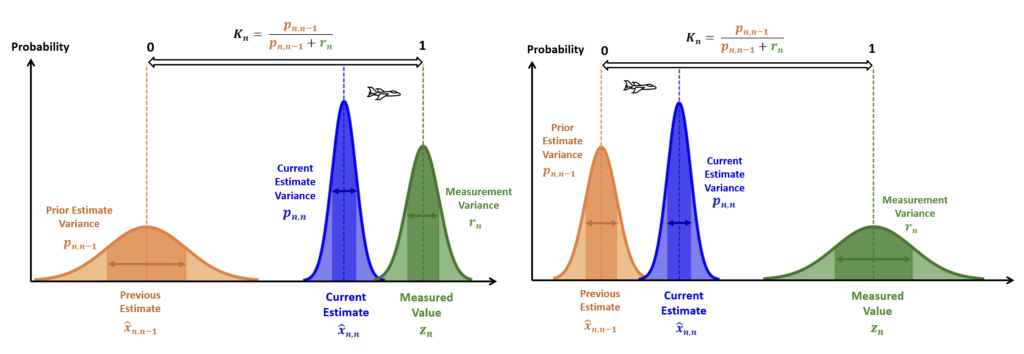
Hoher Kalman-Gain (links): Stärkeres Vertrauen in die Messung. Niedriger Kalman-Gain (rechts): Stärkeres Vertrauen in das Modell.
Dieses Modellierung ermöglicht robustes Tracking, selbst bei unzuverlässigen Messungen oder unsicheren Modellen.

Mehrdimensionale Systeme

Reale Systeme umfassen oft mehrere interagierende Variablen (z. B. Position und Geschwindigkeit in 2D). Der mehrdimensionale Kalman-Filter erweitert die Konzepte durch Zustandsvektoren und Kovarianz Matrizen, um Unsicherheit und Korrelationen zwischen Zustandsvariablen zu repräsentieren. Dadurch kann der Filter modellieren, wie Änderungen in einer Variablen (z. B. Geschwindigkeit) andere beeinflussen (z. B. Position).

Ein praktisches Beispiel für die Anwendung des Kalman-Filters im IMVS ist die Prognose des Energieverbrauchs. In diesem Kontext hilft der Filter, den verbleibenden Batteriestand eines Roboters zu schätzen, indem er über die Zeit den Stromverbrauch und die Spannung analysiert. Durch die Kombination vergangener Daten mit Echtzeit-Sensorwerten ermöglicht der Kalman-Filter genauere Vorhersagen und intelligenteres Energiemanagement.

Tech-Talk: Andri Wild (andri.wild@fhnw.ch), MSE Student und Assistent am IMVS

Blog Beitrag: Simon Luder (simon.luder@fhnw.ch), MSE Student und Assistent am IMVS